【集萃网观察】纺织品设计在引导消费、美化生活和环境方面起着重要的作用，其中，图案设计在纺织品设计中是一个重要环节[1]。传统的纺织品图案设计由专业人员首先在头脑中构思，再通过纸或其他介质把图案表现出来。图案的创作和修改十分繁琐，设计周期较长，难以满足人们越来越快的求新、求美需求。

　　分形几何是现代数学非线性科学中的一个重要分支，通过迭代、递归等算法可产生大量风格迥异、图案奇美、变幻无穷的图形或图像。借助于计算机程序，把这些分形图案显现出来，将可能使其在生物形态学、艺术创作设计等研究应用领域得到更为广阔的发展[1 - 3]。如何将分形图案应用于纺织艺术，已成为纺织行业研究的重要内容。文献[4 - 7 ]把采用分形理论中L 系统方法生成的图形运用于纺织品组织纹路和印花图案设计，均取得了良好的实用效果；文献[8 ]也就分形理论中的Mandelbrot 集 （ 下文简称M 集） 应用于数码纹织产品开发做了初步探讨；但将分形图案用于织物印花设计的研究却少有报道。

　　分形理论中的M 集，其艺术图案产生于函数的不断迭代，通过对M 集基本迭代式进行不同的数学变换方法，运用计算机绘图方法，可得到大量精美的 Julia 集图形。这些图案均适用于纺织印花图案设计的新资源。本文对基于分形理论中M 集变化得到的艺术图形的生成原理和变换方式以及在丝绸印花制品上的应用做了研究。

　　1 M 集分形图的生成原理及实现

　　M 集是分形几何学中的一类典型分形集，是用计算机研究二次复动力系统得到的复杂图形。 1. 1 Mandelbrot 集的定义方法在复平面中，迭代表达式为:

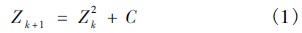
　　式中Z 和C 都是复数，由各自的实部和虚部组成。分离Z 和C 的实部和虚部，则:

　　令初始值Z0 = 0 （ 即Z0 = 0 + 0·i ） ，C ≠0 （ 其中 p 和q 在各步迭代中都保持为常数）。迭代计算中，把前一个Z 值的输出作为下一个Z 值的输入，代入 Zk ← Z2k + C 反复运算，得到一连串的复数。每做一次迭代，新的复数就离开前一个复数一段距离，就如同一个点在复平面上跳舞[9]。

　　1. 2 M 集图形的实现原理

　　在复平面的某一部位，令C 作有规律的变化，对不同的C 值进行迭代，如果计算结果达到无穷大，则C 被着成白色，否则，着黑色，这样就显示出 M 集的形状。若将达到无穷大的点，根据其发散速度的快慢用不同色调来表示，就形成一幅极其吸引人的彩色图形。由系统生成的M 集的图形见图1。

　　2 M 集函数变换方法

　　2. 1 高次幂M 集

　　图1 示出最经典的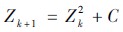的图形，即迭代式中Z2k的幂指数是2，对于k > 2 的广义Mandelbrot集即高次幂Mandelbrot 集，其集图像更为丰富[10]。图2 示出3 阶M 集到10 阶M 集的图形。