集萃印花网 CCEDPW.COM 版权所有
E-mail:YONG_JIA@126.com
Copyright©2003-2020 ccedpw.com. All Rights Reserved
粤ICP备09137305号 客户服务
【集萃网观察】摘要:借鉴BET多分子层吸附模型,建立了织物吸湿多分子层模型。采用c++编程.使用鲍威尔算法对该模型进行求解,得出模型中各个参数值,如水分在织物上的吸附层数、材料的吸湿性能,以及材料吸湿后的干基含水率。通过实验,测出不同材料在一定条件下的干基含水率。比较模拟值与实测值之间的差距,发现该模型能较好的与实验数据相吻合。最后比较分析了不同组织结构织物之间吸湿性能的差异。
吸湿能力对热湿传输过程有重要影响,因此对织物热湿传输模型的研究也都围绕织物的吸湿特性展开。Henry提出一个描述织物中热湿传输过程的数学模型,通过假定纤维中的吸湿量线性依赖于温度和空气的湿度,并且纤维与邻近空气达到平衡是瞬问的,得到了一个解析解。。但该假设离实际的纤维吸附过程太远,限制了它的应用。为了改进上述模型,Nordon和David提出了纤维中湿含量与周围相对湿度的实验表达式,并结几个被Henry忽视的因素给出了方程的数值解,但这些表达式忽略了纤维的吸附动力学原理。Li和Holcombe发展了一个新的吸附率方程,该方程考虑到羊毛纤维的两阶段吸附特性并且结合了更实际的边界条件来模拟羊毛织物的吸附行为。Li和Luo改进了纤维中湿吸附过程的数学模拟方法,羊毛纤维的两阶段吸附过程通过1个统一的扩散方程和2套变化的扩散系数来模拟。本文借用BET方程的思想建立了多分子层的织物吸湿平衡模型,并比较了不同结构的织物之间吸湿性能的差异。
1实验部分
1.1材料与仪器
含涤纶65%、棉35%的13tex双股涤棉混纺纱线,保定依棉集团生产。
涤棉混纺纱线采用梭织法,织成结构缎纹和斜纹织物。缎1:400根/10cm×l80根/10cm:缎2:400根/10cm×220根/10cm:缎3:400根/10cm×260根/l0cm;缎4:400根/10cm×300根/10cm的5枚2飞缎纹织物;缎6:400根/10cm×220根/10cm的5枚3飞缎纹织物。斜2:400根/10cm×220根/l0cm的2上l下右斜纹织物,斜6:400根/10cm×220根/l0cm的3上l下右斜纹织物。
Adventeue啪AR2140电子分析天平;YG601型电脑式织物透湿仪,宁波纺织仪器厂生产。
1.2吸湿实验
按照GB/T9995--1997的《纺织材料含水率和回潮率的测定一烘箱干燥法》,在恒温恒湿箱内进行涤棉织物的吸湿平衡实验,温度设定为20℃,相对湿度依次为20%、25%、35%、45%、50%、60%、70%、75%、85%。
2结果与讨论
2.1测试结果
2.1.1织物的基础数据
表l列出了7种织物的基础数据。可以看出这7种织物的厚度与密度均相差不大,可以认为织物的厚度与密度对比较的结果产生的误差很小,因此在分析比较时,可以忽略不计。

2 . 1 . 2 织物的平衡含水率
表2列出所测织物在不 同条件下的干基 含水率。从实验数据可知,无论哪种织 物均是随湿度的
增大,其吸湿性增大,干基含水率也变大。
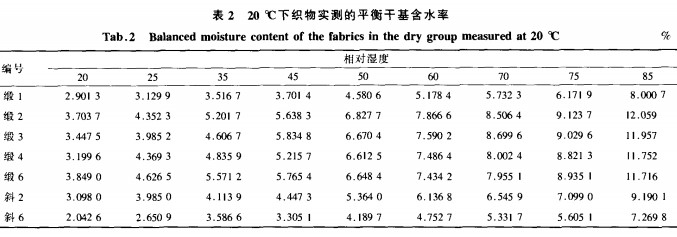
2.1.3密度对吸湿性的影响
图l为在20℃,相对湿度60%的条件下缎纹组织的吸湿曲线。可以看出,同种材料、相同织法的织物在纬密不同时,其吸湿性能随密度的变化呈现一定的变化。在一定范围内,织物的吸湿性随密度的增大而变大,当密度达到一定程度时,吸湿性能反而下降。图中的转折点在纬密220根/10cm左右。由织物的吸湿机制可知,织物疏松时,吸湿主要反映的是材料本身的吸湿性,类似纱线的吸湿;当密度达到一定程度时,织物表面就会产生凝聚现象,主要原因是排列紧密的纱线出现了毛细管现象,湿汽会凝聚,反映出的宏观现象就是织物的吸湿性能提高,但当织物过于紧密时,凝聚现象就会降低,吸湿性能就会减弱。
2.2模型概述
1938年,Brunauer、Emmett、Teller等人将单分子层吸附的Langmuir理论加以扩展,提出了多分子层吸附理论,它包括单分子层和多分子层吸附。
多分子层吸附理论的基本假设为:1)固体表面是均匀的,即吸附活性点分布均匀,吸附能力相同;2)被吸分子之间无作用力,吸附可以是多分子层的,但第1层的吸附与以后各层的吸附有本质的不同,第1层的吸附热也与以后各层的吸附热不同,即第2层以后的各层吸附热接近于气体分子的凝聚热;3)每层的吸附与脱附处于动态平衡。
根据多分子吸附理论,可使用下面的模型对织物吸湿平衡时的吸湿量进行描述:

2.3模型参数估算
使用鲍威尔算法,对模型的3个参数进行估算。使用C++代码编写程序,对实验所用织物进行多分子层吸附模型的非线性回归,估值结果如表3所示,其中R2为将估算的参数代入模型(1)的模拟值与实测值的相关系数。
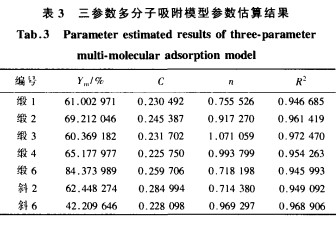
从表3的数据可以看出面料水分吸湿的层数都在1左右。C值在0.2~0.3之间,彼此相差不大,因为C值在理论上只与材料的性质有关。表4是计算出来的模拟值。
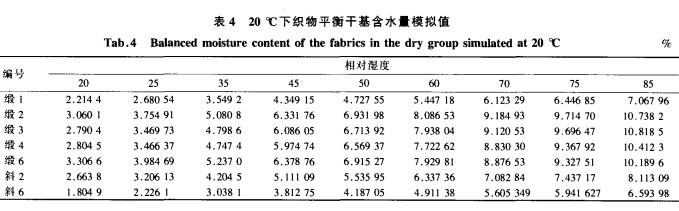
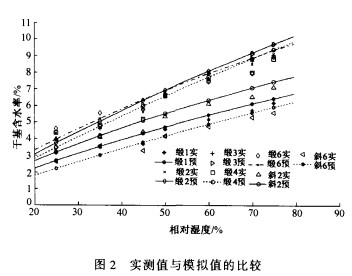
图2比较了7种织物实测值与模拟值的关系。可以看出模拟值与实验值吻合较好,两者变化趋势相同,吸湿性能呈曲线变化。从以上各个织物的吸湿性能来看,在温度为20℃、相对湿度为85%的条件下织物的干基含水率只在10%左右,可见织物的整体吸湿性能比较弱。其原因是:以上各个织物所用的材料是涤棉混纺纱线,材料的固有吸湿性能对织物的吸湿性有重要影响。
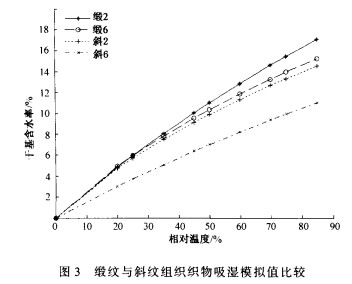
由图3可看出相同材料的织物在经纬密度一致(400根/10cm×220根/10cm),组织结构不同时,平衡时缎纹的干基含水率比斜纹要高。这说明缎纹组织具有较好的吸湿性能,斜纹组织相对较差。
该模型能够较好的模拟某类织物在给定条件下的吸湿性,且能够预测出一定温度和相对湿度下的平衡含水率。该模型的机制应用了BET多分子层吸附理论来研究织物吸湿性能,认为织物的吸湿符合多分子层吸附理论,通过模拟得知,该模型能较好的与实验数据相吻合。织物的结构一致时,织物的经纬密度也是影响织物吸湿性能的重要因素。
3结语
模型的选取与建立是个关键问题,要考虑很多因素,织物吸湿多分子层模型是借助BET模型思想而建立的,认为织物的吸湿满足多分子层吸附理论。
1)该模型的模拟值与实测值吻合较好。
2)给出了模型中3个未知量的具体数值,其值因织物的不同而不同。
3)织物平衡时的干基含水率与织物的经纬密度有关,在一定范围内,密度越大,平衡时的干基含水率越高,密度达到一定值后,干基含水率反而下降。
4)织物的经纬密度相同时,在相同条件下缎纹组织明显比斜纹组织的吸湿性能高。
借鉴BET方程而建立的织物干基含水率模型,能够较好地反应客观实际,是研究织物吸湿性能的一种重要方法。今后可以从不同机制来建立相关模型,综合考虑各种因素,建立更加完善的吸湿模型。
来源 刘凌杰,杜迎春
